
One of the basic components of any manufacturing system is its Material Handling Systems. We shall first study the different types of material handling systems that are currently in use. Next, we shall pick a common type of MH system, a conveyor, and look at some details of how to go about designing a conveyor system for a factory.
Definition: Material Handling refers to activities, equipment, and procedures related to the moving, storing, protecting and controlling of materials in a system.
Why study MH ?
In a typical factory, MH accounts for 24% of all employees, 55% of the space, and 87% of the production time.
It accounts for between 15% to 70% of the cost of a product.
Definition:
MH means providing
the right amount of
the right material
at the right place
at the right time
in the right position
in the right sequence
for the right cost
Some of the above points are quite obvious, others require careful planning.
Right Amount:
This relates to two fundamental issues: how much inventory we need to maintain for different parts/components/modules/products ?
How much WIP must be running through the system ?
The first question will be handled in a future lecture. the second is related to lot sizes and throughput rates:
Exmaple [Hopp & Spearman, p289]
An assembly plant had implemented Manufacturing cells. Castings arrived at the cell from the foundry, and the operations performed were: drilling, machining, grinding, and polishing. The total time to process the parts was less than 1 hour. the company was happy that by placing the processes in a cell, they could reduce the total cycle time from few days to one hour.
Quite impressive, until it was noticed that the batch size for the cell was nearly 10,000 parts. Thus the foundry would deliver 10,000 part batches using a fork lift. Then the cell would manufacture the parts, at the rate of approximately 250 part per hour. Once the lot was completed, the fork lift was again called to transfer the lot to the assembly station.
Question: What is the real processing time in the new arrangement ?
Question: Why does this problem arise ?
Answer: Because the Process Batch size is assumed (incorrectly) = Material Handling Batch Size.
Therefore, one way to reduce the WIP of the Assembly System (not the overall manufacturing system!) would be to reduce the MH Batch, to,say 1000 parts.
How does this affect the design of the Manufacturing System ? MH equipment used to transfer smaller batches can be different; MH traffic rate increases to 10 times of the previous rate.
Trade-offs in Batch sizing for MH:
Right Material:
It is important for the MH system to deliver the proper material. Typical cause of problems may be; Look-alikes (e.g. Red T-shirts of "XL" size and Red T-Shirts of "XXL" size; or M4 screws with slightly different screw head shape etc.)
Methods of identification: Coding, Visual
Techniques for coding: Bar codes, Alphanumeric codes stored and recognized by magnetic strips or visual recognition.
Visual Techniques: Human vision, Optical camera vision and recognition systems.
Right Sequence:
This is an important step in design of manufacturing systems as well as in their operation. Materials delivered in the wrong sequence will directly result in increased WIP (Why ?)
Conclusion: Product design, and Process Planning should be done, if possible, BEFORE the layout of the factory and the MH system is planned. For mixed product systems, where multiple products need to run through the same processing line, the line should be designed to minimize the total amount of loop-back movement of materials. Similarly, in assembly lines, the sequence in which the parts arrive at the assembly station should match the sequence in which they are assembled. One example where this becomes very important is palletizing stations where pallets are bing loaded with a particular part/product mix.
Right Orientation:
Especially important for automated MH systems, or assembly systems. Typical assembly heads can only handle parts presented to them in a given orientation. Often, special devices and tracks are sued to maintain the parts/WIP in a given orientation as it travels along the MH system.
Orientation/Feeding for Small parts: vibratory feeders and tracks are commonly used in mass production. For mixed batch sizes,
our group at HKUST is developing MPATS ( Modular, Parametric, Assembly Tool Set). This tool set comprises of vibratory feeders, rotary feeders, feed tracks, multi-layer multi gripper robot end-effectors).
Hardware Details
We now look at the different types of MH hardware. In most cases of MH, we talk in terms of the handling of a UNIT LOAD. This is one unit of the material that will travel through the section of the Mfg Sys in which we are interested. Typically, the Unit Load may be one part, a few parts of the same type, a pallet with a mix of parts, or even a container to be shipped out of Container Terminal No. 5 in Kwai Chung.
Hardware Categories and Examples
[source: Tompkins et al, Boothroyd et al, Joneja et al]
Flat belt, Telescoping belt, Troughed belt, Magnetic belt
Deflector, Push diverter, Rake puller, Moving slat, Pop-up skewed wheels, Pop-up belts, Pop-up rollers, Tilting slats, Tilt tray, Cross belt, Bombardier sorter
Rotary feeders
Vibratory bowls
Vibratory linear feeders
MPATS
Hand truck, Hand cart, pallet jack, Walkie stacker
Pallet truck, Platform truck, Tractor trailer, Counterbalanced lift truck, Straddle carrier, Mobile yard crane
Automated Guided Vehicle (AGV) [Unit load carrier, Small load carrier, Towing vehicle, Assembly vehicle, Storage/Retrieval vehicle]
Automated electrified monorail
Storing Transfer Vehicle
Jib crane, Bridge crane, Gantry crane, Tower crane, Stacker crane
Block stacking, Pallet stacking frame, Single deep selective rack, Double deep selective rack, Drive-in rack, Drive through rack, pallet flow rack, Push back rack, mobile rack, Cantilever rack
Walkie stacker, Counterbalance lift truck, Narrow Aisle vehicles
Bin shelving, Modular storage drawers in cabinets, Carton flow rack, Mezzanine, Mobile storage
Picking cart, Order picker truck, Person-aboard automated R/S machine, Robot
Carousels, Vertical lift module, Automatic dispenser
The references I have mentioned carry nice pictures of each of these types of equipment, along with descriptions: It may be a good idea to know each of these, and understand under what kind of conditions is it feasible and recommended to use which of them.
The 20 principles of Material Handling System Design (adapted from the guidelines of the College-Industry Council on Material handling Education).
Designing MH systems
As you have seen, to study the design of each of the categories mentioned above will take ages, and serve not much purpose. We take the example of the design of a conveyor based system, to get some idea of the METHODS that are useful in making design decisions.
Conveyors can be categorized in several different ways. On the basis of their conceptual layout, we use the following two categories: (1) Open vs. Re-circulating. Open conveyor systems have fixed material entry and exit points. Materials go across the system only once, and need to be carried back to the entry point and re-loaded if they need transportation across the system. Re-circulating conveyors form a closed loop, such that materials once loaded can travel on them for ever. (2) Uni-directional vs. Bi-directional. Most conveyors operate uni-directionally, that is, at a given point on the conveyor, the materials can only travel in one direction. Some sophisticated conveyors (for example, the Bosch Flexible Assembly System in our Manufacturing Systems Lab) are bi-directional. Bi-directional conveyors are often modular in structure. Each module forms one segment of the conveyor, and can be individually switrched to go forward or backward. Therefore these systems need some form of automatic control to managed proper material flow between stations in a shop. The figures below show schematics of typical uni-directional (that is, the conveyor cannot reverse its direction) conveyor systems.

Typical applications:
Open single lines: assembly lines, chemical plats, etching operations, for example to make lead-frames for electronics chips, etc.
Double-sided open lines (these can fit more operators per unit length of conveyor): assembly lines
U-shaped open lines: typical for manufacturing cells. Notice that a cell may have fewer operators than the number of machines.
U-shaped assembly lines (very compact, single loading and unloading point (often an advantage for material handling): Assembly lines.
Multiple Lines: typically used for a product with several sub-assembly operations. Each line performs a single module of the product, and the main line assembles the final product.
The following figure shows two basic types of re-circulating (closed loop) conveyors. These are quite popular in several machining shops, and sometimes also in assembly shops. The nice feature is that jobs that cannot be directly worked upon can just remain on the conveyor. When the processor/machine becomes free, it just waits for the job to return and then picks it up and performs the operations necessary. Thus the conveyor also acts as a buffer. Another nice feature is that there is complete flexibility to place the loading and unloading stations at any point along such conveyors. There may be one or more of loading and unloading stations, or there may even be a common load/unload point. The shape of closed loop conveyors can be modified to meet the shape of the room/shop-floor, or to go around some large machines, etc. The most common shapes are rectangular, or semi-circular ended rectangles.
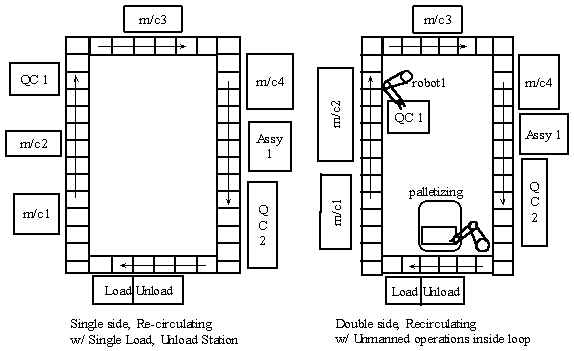
Quantitative models for conveyors: Once the conveyor type has been determined, its design requires determination of conveyor width, speed of operation, power requirements, length and shape. We now look at some simple methods and guidelines to determine some of these parameters.
The first set of guidelines of interest are attributed to T. T. Kwo. Kwo's guidelines for closed-loop, irreversible conveyors are:
The shape of the conveyor is often determined by two factors: (1) Existing machines and their relative positions (which are typically determined by the sequence of operations on the parts;) and (2) Existing space and floor-plan of the shop floor.
The width of the conveyor is determined by the size of the part carriers. Usually, parts are kept on bins or carriers which travel above the conveyor. These carriers are usually rectangular. Their size is determined by two factors: the size of each part, and the number of parts being carried on each carrier. Given the size of the carrier, it is easy to determine the width of the conveyor. Typically, if it is important to retain a fixed orientation for each carrier, then it must travel in the direction along its longer side; thus the width of the conveyor is just greater than the shorter side of the carrier.
Length of the conveyor
Single Part per Carrier case (deterministic). Let:
Required loading speed = l parts/min
Conveyor length used by each carrier = d (= carrier length + allowance)
Number of unloading stations = Mu
Average unloading speed = m parts/min
Conveyor velocity = v
If a carrier passes a free unloading station, it will be unloaded. If all unload stations are busy, the carrier will continue to recycle on the conveyor.
Condition 1. If units arrive at the loading station faster than they can be loaded, the will be blocking. This condition occurs when:
l
< v/d
That is, one would set the conveyor velocity at a level such that the carrier arrival rate (v/d) is greater than the part arrival rate, l.
Condition 2. The unloading stations must be able to handle the conveyor traffic. In short, this means that Mu . m > l.
Also note, that if l.d/v = 2/3, then, in the steady state, every third carrier will be empty. Therefore, an unloading station
with unload times between d/v and 1.5d/v will have sufficient capacity. However, it will not be ready to unload every second consecutive part that arrives. In the steady state, there will be several filled, completed jobs always circulating on the conveyor.
Multiple parts per carrier case [Muth's model]:
Now we look at a more complex model, where each carrier can carry more than one units of material. As the carrier goes past a workstation, it may pick up a unit, and work on it. When the processing is completed, it will put the part down on the next carrier that comes to it, with some free space to load the material. Over a period of time, such systems operate in steady state, with a periodic nature. If I stand at station-R, and look at the situation, it will load R1 parts on the first carrier going past it; it will load R2 parts on the next one; R3 on the third, and so on. Then, after P carriers go past, it will repeat this cycle of loading R1…R2…R3….RP parts. Of course, Ri can be positive (loading), or negative (unloading).
Muth's model for this situation is discussed below:
Number of stations around the conveyor = S
Number of carriers on the conveyor = K
Number of parts picked/placed by Station i on the n-th carrier = fi(n)
If fi(n) is +ve, parts were loaded, if -ve, they were unloaded.
Each station will pick/place a constant number of parts from every p-th carrier passing in front of them:
fi(n) = fi(n + p), for each i.
Note: p is called the periodicity of the system.
In steady state, there should be no build-up of material in the shop => The sum of all material loaded/unloaded from all carriers = 0. This is given by:
![]()
The n-th carrier, the total number of parts loaded/unloaded as it goes around the S-stations is:
![]()
Note that when the n-th carrier returns to the S-th station, already K more carriers have passed this stations, therefore, to station-S, it appears that this carrier is the n+K-th carrier. We position ourselves at station-1, and then, carrier n = carrier n+K = carrier n+2K etc.
Here are some of Muth's observations:
The physical meaning of the above two conditions is basically that the load on each carrier remains relatively uniformly balanced during long term operation.
One can further follow the carriers around the system, and write the following equation for the material handled by each carrier as:
H1(n) = H1(n - r) + F1(n)
Note: Each time a carrier goes the full loop, its position increases by r. The carrier which was (n-r), after it goes one loop, will become carrier (n). Further, in going through this loop, it will gather F1(n) units.
The procedure:
Use the equation above to solve recursively for:
H1*(n) = H1*(n - r) + F1(n)
Hi+1*(n) = Hi*(n) - fi(n)
c = minimum over all i, s[Hi*(n) ]
This is a laborious procedure, and is best performed using a small computer program. Using such a program, one would typically test for several different number of carriers, assign loading patterns (period, number loaded per carrier), and thereby calculate the maximum carrier capacity required. From all the different trials, the best configurations can be obtained.
Example:
Consider a case with 1 Load station, 1 Unload station, 9 carriers, and period of 7.
For station 1, {f1(n)} = { 1, 1, 2, 2, 2, 1, 1}
For station 2, {f2(n)} = { 0, 0, 0, 0, 0, -5, -5}
Thus,
F1(n) = { 1, 1, 2, 2, 2, -4, -4}
r = k mod p = 9 mod 7 = 2.
Assign:
H1*(1) = 0
H1*(3) = H1*(1) + F1(3) = 0 + 2 = 2
H1*(5) = H1*(3) + F1(5) = 2 + 2 = 4
H1*(7) = H1*(5) + F1(7) = 4 - 4 = 0
To obtain H1*(9), we note that p = 7, so H1*(9) = H1*(2). Thus,
H1*(2) = H1*(7) + F1(2) = 0 + 1 = 1
H1*(4) = H1*(2) + F1(4) = 1 + 2 = 3
H1*(6) = H1*(4) + F1(6) = 3 - 4 = -1
So: {H1(n)} = { 0, 1, 2, 3, 4, -1, 0}
Next, using H2*(n) = H1*(n) - f1(n), we get:
{H2*(n) } = { 0, 1, 2, 3, 4, -1, 0} - { 1, 1, 2, 2, 2, 1, 1,} = { -1, 0, 0, 1, 2, -2, -1}
From which, c = -2 (when i = 2, and n = 6), and B = 6 (for i = 1, n = 5).
Therefore: Each carrier must be large enough to carry 6 units.
Note: Since carrier arrival rate at a station also depends on the conveyor speed and the distance between stations, the sequence fi(n) changes with a change in either of these, usually resulting in quite different solutions.
While the above procedures are interesting, it is difficult to predict how good the solution is, since there is often a stochastic element in the operation of the manufacturing system. In general, it is easy to set up simulations of a conveyor, and test different scenarios using stochastic numbers to obtain pretty good results. Therefore a strategy to design conveyors would involve the steps:
References:
Facilities Planning, Tompkins, White, Bozer, Frazelle, Tanchoco, Trevino, pub. John Wiley, 2nd Edition.
Assembly Automation and Product Design, Boothroyd, pub. Marcel Dekker
Factory Physics, Hopp and Spearman, pub. Irwin press
Modeling and Analysis of Mfg Sys, Askin and Standridge, pub. John Wiley.