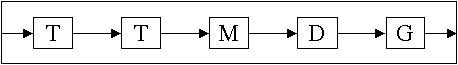
Manufacturing Systems Design
The topic of Manufacturing Systems Design is a broad, inter-disciplinary one, which covers aspects from almost all other specialized topics one may choose to study in engineering. We shall study aspects of it that are felt to be important. The concentration will be more on those aspects of the topic that we can study through formal, or systematic methods.
A systematic method typically uses models. In other words, we will always endeavor to "model" a real situation. What is a model ?
We say that X models A, if X is able to answer questions about A. How good our model is depends on (a) the range of questions our model can answer, and (b) the accuracy/reliability of the answers.
When we use models as tools, we must clearly understand the domain in which the model is accurate enough for our purpose. A poor understanding of the model will result in errors.
Models are not a new concept. Newton's law of gravitational attraction between entities with finite mass models an aspect of the interactive behavior between these entities. This is an example of a deterministic model. Several of you have built simulation models of manufacturing systems using software tools that combine logic and statistical data.
Since it is common for us to think in terms of objects (physical, or abstract) and actions that can be performed either by such entities, or by us, we often follow such metaphors to create models using entities and actions (or functions).
We would like to think of Manufacturing Systems in terms of physical resources and functions that define the operations carried out in any MS. Typical functions in our studies include:
Such a break-up of systems has underlying assumptions about what knowledge/information resides with which function. There are other (e.g. object-oriented) techniques of modeling of systems where the information storage and flow are another important function.
In other words, there are different ways to model the same physical reality. Which is better ? Depends on how well it is implemented, and how well the person(s) using the model know its strengths and limitations.
The domain of manufacturing systems is large, in terms of size, complexity (of products, processes etc). Consequently, models to answer complex questions about their predicted behavior are also complex. This is especially true for quantitative models. It is therefore convenient to qualitatively break down such systems into categories, and develop different models for each category. Even within each category, if possible, we strive for functional break-up. The need for such simplifications is due to the limitations of our models. Quantitative models are essentially backed by logic and mathematics. Only a limited mathematical models can be solved conveniently, even using the best of computers.
At the highest level, we can assume an MS as a system into which some materials flow, and inside which some/all of these materials are transformed before emerging out as products. Therefore, the concept of "materials" is quite fundamental to any MS.
Accordingly, it has been the convention to categorize MS in terms of HOW the materials move when they are inside the system. Obviously, this is related to how the facilities inside such a system are laid out. In these terms, we classify MS into four types:
Product-based,
Process-based,
Cell-based (or Group Technology based), or
Fixed Position.
These are systems where the MS is designed totally based on the product that it outputs. The product is analyzed, the materials and equipment required to create it are identified, and the MS is designed such that the incoming materials flow through a series of stages. At each stage, the subsequent planned operation is carried out until the final transformation of the materials into product. Examples of such systems are assembly lines, or transfer lines. Since the processing stages are laid out in a series, such an MS may also be called a serial system.
Such systems are common when the MS is engaged in manufacturing a few (or even one) kind of product, but in large volumes. Under these conditions, this layout tends to give low throughput times and low work-in-process (WIP) inventories.
An example of a Product based layout
We can identify all the different operations that need to be carried out on the material(s) while they are in the MS. Each operation can be achieved by some kind of an operator (usually a machine). This gives us another way to lay out our MS: collect all operators (machines) that are 'similar', and put them close to one area (e.g. in the same room, or the same zone of a factory). Obviously, similar operators perform similar tasks, or processes. This type of a layout can be called a process-based layout.
It has been estimated that over 75% of manufacturing occurs in batch sizes of less than 50 items [Askin et al]. I personally doubt the accuracy of this statistic for HK-based industries [and welcome any student to take up a project to give us an estimate !]. However, such conditions can (and do) exist. Here, we need machines that perform a variety of operations on an even larger variety of jobs. A common way to set up an MS operating in such conditions has been to set up departments, or areas with similar machines. In particular, if the operations are primarily machining operations, we call such an MS a job shop.
As we shall see when we try to set up mathematical models for, say, operation scheduling in such an MS, the search space for 'good' solutions increases exponentially with the problem complexity. In general, it is agreed that such systems result in sub-optimal operations, long throughput times, and large WIPs.
On the other hand, in custom production situations, such layouts facilitate process knowledge accumulation. Grouping of similar machines can also allow higher machine utilization, since extra capacity need not be spread across the MS.
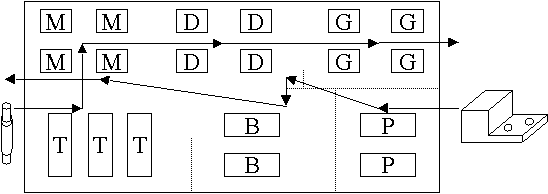
A Process-based layout. Each part has a different, fixed route through the departments.
In the last few decades (perhaps largely coincident with the rising importance of IE), the important concept of Group Technology has been exploited in several ways. One application was in the design of MS, where traditionally process-based systems could be re-organized into a set of smaller sub-systems, each of which specialized in specific task-sets (rather than a single task). These sub-systems, called Cells, operate more-or-less like small product-based systems within the larger MS. The idea of cells is a useful one in the design of MS. The idea of Group Technology (GT) is an even more important one. We shall study both in some detail in this course.
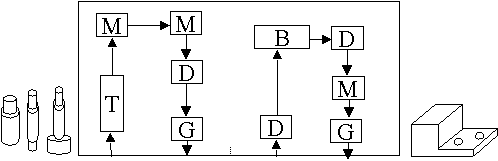
A Cellular layout, with different part families assigned to different cells
Several infrastructure type of productions have a different model for the MS. Here, we look at the system as if the materials (or some of the materials) stay in a fixed position, and the MS travels to and around the materials, operating upon it until it is transformed. Examples include ship-building, aerospace industries, etc. We shall largely ignore such systems in this course, and focus on the first three types of MS.
Important Concepts
In this brief section, I shall emphasize some fundamental concepts that are central to the concept of every Manufacturing System. They are familiar, but it is important to list them during our introduction, for completeness.
(a) Interchangeability
(b) Division of labor
(c) Group Technology
Following are some of the principles important to remember when we build models, or verify them. Keeping these principles will give us intuition that can help in verification, and sometimes simplification of models that we build. Violating them may result in illogical or inconsistent models for MSD.
(a) Little's Theorem: L = l W
L = average number of items waiting in a system,
l
= the average arrival rate, andW = average time spent by an item in a system.
[Also called Little's Law].
This theorem applies to any system in steady state, even stochastic ones. An intuitive (and incomplete) proof of this follows from the following figure:
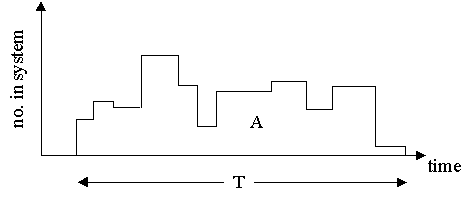
[source: Little, J.D.C., Tautologies, Models and Theories, IIE Transactions, vol 24 no 3]
The area under the curve in the above graph, A, represents the total time spent by all items within the system over time T. Since the average arrival rate of items is l, the number of items arriving (or leaving, since the system is in steady state) in time T is l T. Thus the average waiting time, W, for an item is:
W = A/ l T (1)
Of course, the average number of jobs in the system can directly be computed from the graph as:
L = A/T (2)
Eliminating A/T from (1) and (2) gives Little's theorem, L = l W. The nice thing about this theorem is that it can be applied to several real-life situations, especially in the behavior of MS. The equation holds true for all systems in steady state, whether it is the entire factory, a work-cell, or a machine. The formula is equivalently written as:
WIP = Production Rate X Throughput Time
The above terms are commonly understood by all plant managers, who can then use it to make planning decision. For instance, by pushing more raw materials into the plant, you increase the WIP, which in turn should increase the Production Rate. Of course, once the production rate increases to a limit where one or more processors are working at 100% utilization, the Throughput time starts to increase, without any further change in the Production rate. More items are now waiting in queues at different points within the system.
Little's law is useful, since several models for analysis of queues yield either L, or W, but not both. Given one, if the steady-state assumptions hold, we can calculate the other.
(b) Probability theory and System reliability
As systems tend to increase in size (that is, as number of operators increase), the reliability changes. This change may be upwards, or downwards, depending on the use of every additional operator. Probability networks provide a common mathematical model to study these effects. Obviously, application of the proper probabilistic model requires some amount of care. Bayesian models, for example, require a good estimate of a priori probabilities (to estimate P(A /B), one must know the a priori probabilities of events A and B.) Without going into details, let's make note of some simple results that should guide our intuition.
(i) In serial systems, probability of failure (equal to (1 - reliability)) increases as number of operators increase.
If pi is the probability of failure of the i-th independent operator, system reliability will be:
rsystem = P(1- pi), i = 1..N
How do we increase system reliability ?
Either by increasing the individual operator reliabilities, or by adding "parallel" or "alternative" operators. If we find that the j-operator causes system failures due to frequent breakdown, we could add a parallel component, j'. In this case, the reliability is given by:
rsystem = ( 1 - p1)(1 - p2) …(1 - pj-1) rjnew (1 -pj+1)…(1 - pN)
where rjnew = 1 - pjpj'
[Since probability of failure of new station = pjpj']It is easy to see that 0 <= rjnew <= 1, and that rjnew >= rj, rj'
On the other hand, if new operators are added to the system, the overall system reliability can only decrease.
Typically, it is not easy to get accurate estimates of pi for some components. One reason is that equipment breakdowns are time/usage dependent. The second reason is that breakdown data must be collected over a long period of time to get these estimates. In estimating workstation reliability, one must further estimate the interplay of operator, his experience, machine etc.
(ii) Base rate errors
Design and operation of systems require decisions. For example, you may need to decide which manufacturer's machine you buy to perform a function. You may use the data about the maintenance costs of such machines in your other plants. The application of prior knowledge to decisions requires some care, as illustrated by the following example.
90% of the taxis in HK are red taxis, and the remaining 10% are green. One night, there is a hit-and-run accident involving a taxi. The witness said that the taxi was a green taxi. The witness was tested, and found to be quite reliable: he was able to identify the correct color of taxi (in night-time) 85% of the time.
What is the likelihood that the taxi in the accident was green ?
Note: Using Bayes' Law, we have:
P(thinks taxi is green, and taxi is red) = P(thinks taxi is green | taxi is red) P(taxi is red)
= 0.15 * 0.9 = 0.135
but
P(thinks taxi is green, and taxi is green) = P(thinks taxi is green | taxi is green) P(taxi is green)
= 0.85 * 0.1 = 0.085
In other words, the witness is more likely to be wrong !
(c) System Planning and Complexity
Design as well as operation of any system requires making a series of choices. At each point where one makes a decision (selects one option from a set), a particular combination of conditions are being explored. We often model such decisions as a network of choices (or a graph). If we stop to make a choice at N different stages of design, and at each point, we had M different options to choose from, we had a total of MN alternative solutions. In terms of the search graph, this number grows very rapidly as either N or M grows. Moral: design is complex.
The practical implication of this observation will hit us at each stage of this course -- almost every model that we shall build will require searching over incredibly large number of choices to find "good" solutions. We think of the goal of IE to fond optimal solutions. We shall see that we seldom reach this goal, and use 'rules-of-thumb', or heuristics, to point us in the right direction.
(d) Temporal aspects (Designers must be aware of the time axis):
(d1) Wear of equipment
One aspect that must enter into design considerations is that equipment and products wear out. Over time, performance and reliability change. If we design a system without this notion explicitly accounted for, the design will fail.
(d2) Obsolescence
The second important temporal aspect is that technical advances will make most equipment (hardware, software, and even personnel skills) obsolete. Every design must be aware of this fact. It is not sufficient to evaluate a design of an electronics assembly line based on the assurance that your automatic assembly machine will last 10 years. Perhaps it will, but four years down the line, your competition may be able to buy a machine twice as efficient/fast as yours. Recognition of technology trends is therefore important in design.
Methods For Manufacturing Systems Design
There is not much agreement whether the activity of design is systematic or not. Those who believe that it is NOT often use the word 'creative' to describe design. Much literature can also be found dividing design into creative (or conceptual) and systematic (or analytical) partitions. There are others who believe that there is an underlying systematic 'sense' to all design -- and that the best designs can be generated using an approach that can be coded (that is, there is some algorithmic approach to design). Whether one believes this claim or not, some of the principles set forth by the proponents of these theories are useful tools to design. We shall spend some time on the study of such systems as Suh's Axiomatic Design and the TIPS systems.
The emphasis of the above approaches appears to be more on the 'conceptual design' phase. Given a conceptual design, there is little doubt that analytical tools become indispensable to make good decisions. Such tools are often based on mathematical systems, with sound foundations on logic. We shall see many such models -- either deterministic, or stochastic. Complex systems with stochastic elements involved can also be simulated using computer models. A good understanding of the underlying statistics can often yield good estimations of important design variables through such simulation.
Once again, it must be emphasized that most mathematical models of complex systems are complex. Even the ability to formulate such a problem mathematically does not guarantee that we can solve the model usefully. A simple example is the job-assignment problem.
EXAMPLE
Suppose we have three machines, each of which can perform any of three jobs. The cost of performing a job by a machine is known (see table below). Find the least cost assignment of jobs to machines.
|
Machine |
|||
|
JOB |
1 |
2 |
3 |
|
1 |
10 |
25 |
12 |
|
2 |
13 |
5 |
12 |
|
3 |
8 |
13 |
21 |
Let's say that a set of variables Xij is used to denote whether a job i is assigned to machine j. If Xij = 1, job i is performed on machine j; otherwise, Xij = 0.
We can then formulate the problem as follows:
minimize sum{i,j}( cij Xij)
Subject to:
sum{i} Xij = 1 // since machine j must take only one of the jobs;
sum{j} Xij = 1 // since job i must go to only one machine
and of course, all Xij's are 0 or 1.
Now a computer program can be generated easily to solve this problem optimally. After all, it only has to consider 3! possible permutations of jobs on machines.
Unfortunately, if I use the program for a problem where the number of machines and jobs is larger, it could take a long time to obtain the optimal solution (since the combinations increase exponentially, being a function of the factorial of the problem size).
Later, we shall see how such problems are solved using heuristics, which do not guarantee optimality, but can do better than using a naïve decision making process.
On the face of it, the example above appears to be concerned more with operational decisions on MS, not with the design. Why then are we interested in it ? Because every MS design that we propose must be evaluated, to guarantee that it shall perform within some design specs that have been specified for it. In other words, every design option must be analyzed. To do so, one often needs to model it. Hence, modeling and analysis are a significant aspect of design.
Reading:
Askin, RG, Standridge, C.R., Modeling and Analysis of Manufacturing Systems, Chap 1
Little, JDC, "Tautologies, Models and Theories: Can we find Laws of Manufacturing?," IIE Transactions, v 24, n 3, July 1992