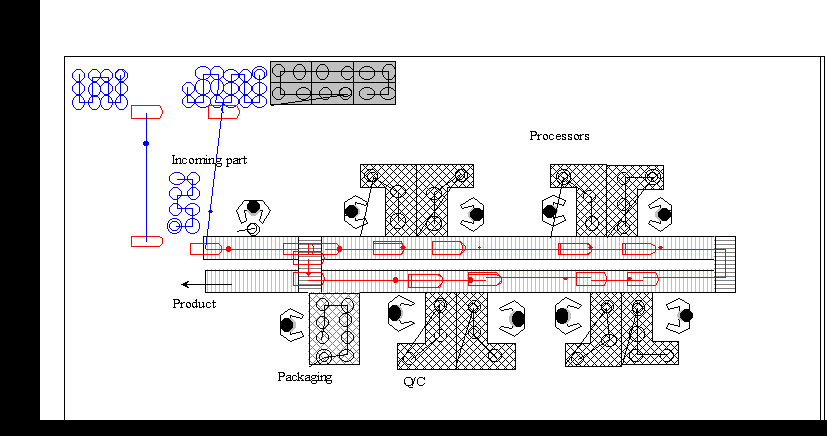
Serial Systems
All assembly lines rely heavily on two important principles: Interchangeability and Division of labor.
We shall consider systems that have physically a series of workstations through which the material passes. The obvious design decisions then include:
Typical serial systems are assembly lines or transfer lines. In assembly lines, a base, or partial assembly of the product travels to each station on a conveyor. The product is held stationary at this point, either by stopping the line, or by a stopper, or by lifting it off the line. Operation(s) are performed, on it, and it is released to travel to the next station. We assume that assembly operations are reliable, in the sense that there are no break-downs in equipment, and the processing time variability is relatively small.
Transfer lines are also serial systems, but usually refer to capital intensive production lines. The oldest example is an automobile manufacturing plant, where each workstation has expensive production tooling (e.g. a welding robot). The operation times between units may vary (setup times, tool or machine break-down, or operator unavailability are common reasons).
We shall mostly restrict ourselves to assembly lines.
In either case, the design of the line essentially requires a break-down of the product assembly operations into small work elements -- basic steps by which value is added to the work-in-process.

The U-shaped line is quite common in many assembly systems. Very often, if each workstation requires components to be delivered to it, the delivery is along the center of the line, in which case the work-stations are also located along the inner side of the conveyor. We shall go into the different possible geometric configurations of serial lines later -- when we look at layout planning.
The first task for the designer is to produce the process plan. This includes specification of (a) the individual work elements; and (b) precedence requirements between the work elements.
The figure below shows the general schematic of the processes.
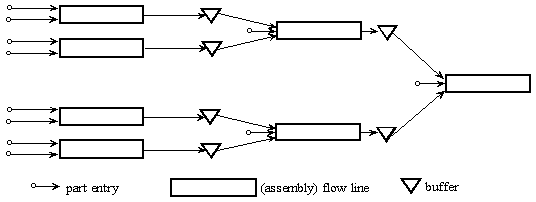
[figure source: Askin and Standridge, p 35]
In most serial systems, each station in a line is really a set of parallel, identical stations. Each workstation in a set of parallel stations performs similar activities. This is a common layout when a series of product variations are being manufactured (e.g different colors in a T-shirt sewing line).
The buffers are necessary to ensure that no workstation gets "starved" -- since there are often variations in process times (especially for manual lines). The important decision in the design process is to ensure that production rate matches the demand. Since it is likely that work elements take different times, this results in the problem of assembly line balancing. We shall describe this problem, and see if we can solve it.
EXAMPLE
Computer Assembly: Production rate = 100 units/ hour
Stage 1 : Assemble boards, power supply, cables to frame; [8 min per unit]
Stage 2 : Visual test for proper assembly of all boards and cables; [2 min per unit]
Stage 3: Burn-in testing of assembled unit; [120 min per unit]
It is easy to compute how many parallel stations we need for each stage:
Stage 1: é 8 * 100 / 60ù = 14 parallel stations;
Stage 2: é 2 * 100 / 60ù = 4 parallel stations;
Stage 3: é 120 * 100 / 60ù = 200 parallel stations.
Of course, designing the material handling system for even such a simple system could be more complex (think of how to route each part to the next stage !)
Let us try to formulate a more general case of assembly line balancing problem. Assume that the work elements are known, and we have a good estimation of the time required for each.
Required production rate = P
Assume that we are investigating the use of m parallel lines.
Then the demand is satisfied if we maintain a Cycle time = C = m/P
We are looking to assign one or more tasks to each workstation, such that no worker has a cycle time exceeding C.
We must perform all the tasks i, and each task takes time ti.
According to the process plan, there could be precedence relations between some tasks. To specify these, we collect, for each task, the task that must immediately precede it:
Set IP = { (u, v) | u must precede v}
[Note: immediate precedence record is necessary and sufficient]
We may restrict some tasks to be done on the same station (e.g. if they need a special, expensive equipment, or special operator skills). Let ZS be the set of every task pair that must share a station.
Likewise, each task pair that must not be done on the same station is stored in the set ZD. (Examples ?)
We use the following binary decision variable:
Xik = 1
(if task i is done on station k), 0 otherwise.
The key to the formulation lies in the following simple observation: The solution with the least number of stations results in the lowest idle time.
[Prove it !]
To minimize the number of stations, we use an artificial cost function, cik, as follows:
Ncik
The objective is to minimize:

subject to
(a) total time taken at any station must be less than the cycle time:

(b) each task is performed on exactly one station:

(c) precedence constraints must be met:

(d) ensure correctness for task pairs that must be done on the same station:

(e) ensure correctness for task pairs that must be done of different stations:
![]()
It is not difficult to see that this formulation captures all aspects of our problem. The clever cost function in the objective ensures that the optimization routine will look for a minimum number of stations (since filling an existing station is guaranteed to be cheaper than putting a task onto a new station).
It is easy to specify a measure for how good our solution is. Assume that K* is the optimal number of stations. In each cycle, the total number of station-time units available are K* C. Also, since one unit of product rolls out in each cycle, the total time used in assembly of this unit = S ti. The measure we look for is the normalized value, called balance delay, defined as:
D = ( K* C - S ti ) / K* C
Question: Is this optimization problem easy to solve ?
In general, no. Firstly, the size of the search space could be large.
Secondly, it is non-linear (due to the ZS constraint).
Algorithms to solve (non-optimal) the Line Balancing Problem
COMSOAL
The approach can be summarized as follows:
Generate a random solution satisfying all constraints, storing the number of stations it needs. Repeat this random generation process, keeping the best solution, and discarding poor ones. The second stage can be aborted if a partial solution is already worse than a previous (better) solution.
One method to implement this approach is shown in the following pseudo-code.
Variables:
COMSOAL Algorithm:
Step 1. Set x = 0, UB = N, C = cycle time, c = C.
Step 2. Start new sequence: set x = x+1, A = TK, NIPW(i) = NIP(i).
Step 3. Precedence feasibility: For all i Î A, if NIPW(i) = 0, add i to B.
Step 4. Time feasibility: For all i Î B, if ti £ c, add i to F;
If F is empty, go to Step 5; else go to Step 6.
Step 5. Open new station: IDLE = IDLE + c; c = C.
If IDLE > UB go to Step 2; else go to Step 3.
Step 6. Select task: Set m = card{ F};
Randomly generate RN Î U(0, 1);
Let i* = é m.RNù th task from F;
remove i* from A, B, F.
c = c - t*i;
For all i Î WIP( i*), NIPW( i) = NIPWW(i) - 1;
If A is empty, go to Step 7; else go to Step 3.
Step 7. Schedule completion: IDLE = IDLE + c;
If IDLE £ UB, UB = IDLE and Store the schedule;
If x = X, stop; else go to Step 2.
COMSOAL Toy Car Example:
Consider the following product, a toy car, whose assembly tasks are shown in the figure below.

[source: Figure 2.4, Askin &Standridge.]
Task chart for Toy Car:
|
Task |
Activity |
Task time |
Immediate Predecessor |
| a | Insert front axle/wheels | 20 | - |
| b | Insert fan rod | 6 | a |
|
c |
Insert fan rod cover |
5 |
b |
|
d |
Insert rear axle/wheels |
21 |
- |
|
e |
Insert hood to wheel frame |
8 |
- |
|
f |
Glue windows to top |
35 |
- |
|
g |
Insert gear assembly |
15 |
c,d |
|
h |
Insert gear spacers |
10 |
g |
|
i |
Secure front wheel frame |
15 |
e,h |
|
j |
Insert engine |
5 |
c |
|
k |
Attach top |
46 |
f,i,j |
|
l |
Add decals |
16 |
k |
Production conditions:
2 shifts per day, 4 hours per shift, 2 breaks per shift (10 minutes each), 4 days per week.
Demand (= production rate) = 1500 units per week.
Cycle time = C = 4* 2 * 220 / 1500 = 1.17 minutes/unit = 70 sec/unit.
The following figure shows the precedence graph for the assembly tasks:

The basic idea of the algorithm is as follows:
Start with the tasks that have no predecessors;
Randomly assign one to the current station;
Since this task is now 'done', if it was a predecessor of any other task, that task can now be assigned. Add all such tasks to the pool of tasks from which the random draw takes place.
Of course, since the current station now only has time remaining = RT = (cycle time - time for assigned task) left, only those tasks will enter the pool which need less time than RT.
If no such tasks exist, we cannot put any other task on this station; start a new station, and continue with the process above.
We can get a clearer understanding of this process by steeping through the example of the toy car, using the following chart, which shows the stepwise execution of the program.


Questions:
How many stations did we need using COMSOAL for the above example ?
On the face of it, it does not look like a good solution -- after all, the final station only has one task assigned to it, and will be idle for most of the cycle. The other stations also have some idle times (how much ?).
Can we answer: what is the minimum number of stations required ?
In general, no. However, we can say the following: The best solution must have K number of stations, where K = (total time of all tasks/Cycle time).
[WHY ?]
In our case, K = é 202/70ù = 3.
At least 3 stations must be used.
RANKED POSITIONAL WEIGHT HEURISTIC
This is another popular heuristic approach to solving line balancing problems for assembly lines. The basic idea is to allot tasks to stations based on their priority. The priority is determined by the total time needed by the task and its successors.
The logic is simple: If we have a large number of tasks from which we can choose to assign to a station, we are more likely to find a (combination) that will minimize the idle time.
From the above, it follows that if we minimize idle time at each station, we should end up with the minimum number of stations.
[WHY ?]
Definitions:
The procedure can then be easily described:
Step 1. For all tasks i = 1…N, compute PW(i)
Step 2. Order tasks by non-increasing values of PW(i)
Step 3. Assign tasks to first feasible workstation according to the ordering of step 2.
We use the toy car example once again, to demonstrate how the method works. The PW(i)'s are computed using the precedence chart.
|
Task i |
S(i) |
PW(i) |
|
|
a |
bcjklghi |
20+6+5+5+46+16+15+10+15= |
138 |
|
b |
cjklghi |
6+5+5+46+16+15+10+15= |
118 |
|
c |
jklghi |
5+5+46+16+15+10+15= |
112 |
|
d |
ghikl |
21+15+10+15+46+16= |
123 |
|
e |
ikl |
8+15+46+16= |
85 |
|
f |
kl |
35+46+16= |
97 |
|
g |
hikl |
15+10+15+46+16= |
102 |
|
h |
ikl |
10+15+46+16= |
87 |
|
i |
kl |
15+46+16= |
77 |
|
j |
kl |
5+46+16= |
67 |
|
k |
l |
46+16= |
62 |
|
l |
{} |
16= |
16 |
Based on this, the order of priority for assignment is as follows:
a d b c g f h e i j k l
The charts below show the assignment sequence for the algorithm.
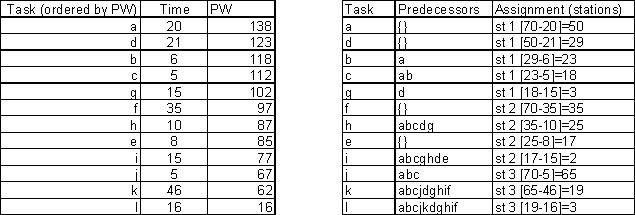
Questions:
In this case, how many stations did we need?
What is the idle time on the stations?
Postscript
The serial systems we modeled above assume a fixed product type. Such systems are quite common among the assembly units you may visit in the SAR region. Later in the course, we shall encounter more complex requirements. The trend towards consumer-centered manufacturing leads to smaller batch sizes, and larger product mixes. Eventually, the manufacturing system requirements under such conditions will complicate the computations. For such a system to operate efficiently, we shall see that the focus must shift more upstream. A better design of the product mix can lead to efficient manufacturing and simplified planning. We shall see some aspects of such problems when we study mass customization.