ADDENDUM to CAD Part I
Notes on Geometry
Geometry: deductive system based on postulates (axioms) and undefined elements.
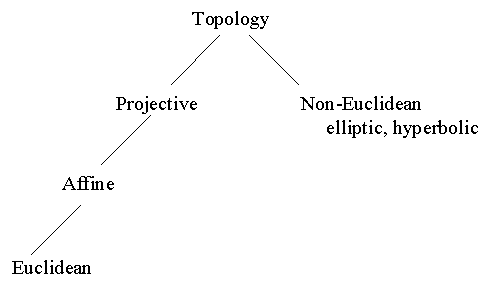
Classification:

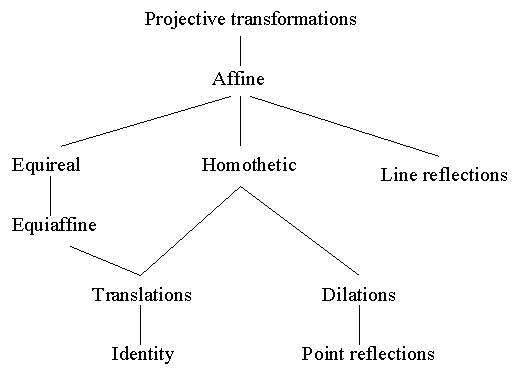
The study of geometry is mostly concerned with the study of properties that remain invariant under a set of transformations. Mathematically, transformations may be classified as follows.
The study of solid models requires some insights into topology. Some terms that you will meet in reading technical works of related topics are briefly mentioned below.
Metric spaces
If X is a set, and we define a mapping d: X x X à R such that
d( x, y) = 0
d( x, y) = 0 iff x = y
d( x, y) = d( y, x)
d( x, y) <= d( x, z) + d( y, z)
Then d is called a metric on X, and ( X, d) is a metric space.
Examples:
D1. X = R, and d = | x –y |
D2. X = R2, d = | x1 – x2| + | y1 – y2|
D3. X = R2, d = {0, if (x1, y1) = (x2, y2); 1 otherwise}
D4. X = R2, d = max( |x1 – x2|, |y1 – y2|)
D5. X = R2, d = Euclidean distance
p-neighborhood: ( X, d) is a metric space and p is any positive number, then the p-neighborhood of any x in X is the set of all points y such that d( y, x) < p.
Open sets: (X, d) is a metric space, and U is a subset of X. U is open if given any point x in U, there is a positive number p, such that the p-neighborhood of x is a subset of U.
By definition, X and {} are open.
Closed sets: (X, d) is a metric space; a subset F of X is closed if cF is open in X.
Convergence and limit points: ( X, d) is a metric space, and S = { sn}, n in N, is a sequence in X. S converges to point y in X if, for any positive number p, there is a positive integer M, such that for all n > M, sn is in p-neighborhood of y.
If sn converges to y, we write sn à y, and y is a limit point of sn.
A limit point of S may not be an element of S.
( X, d) is a metric space, U is a subset of X. A point x is a limit point of U if each neighborhood of x contains some point of U different from x.
A set is closed iff it contains all of its limit points.
The closure of a subset U of X in metric space ( X, d) is the union of U with all of its limit points. We write closure of U as kU.
Properties of closure:
A point x in subset U of X is an interior point if U is a neighborhood of x. That is, U contains an open subset that contains x.
The interior of a set U, iU, is the set of all interior points of U.
Properties of the interior:
Let ( X, d) be a metric space, and U a subset of X. The complement of U, cU = X – U.
Relationships between c, k and i:
Let ( X, d) be a metric space, and U a subset of X. A point x in X is a boundary point of U if each neighborhood of x has non-null intersection with U and cU.
The boundary of U is the set of all boundary points of U, and is denoted bU.
Properties of the boundary of a set:
For most cases, our normal intuition about closure, interior and boundaries are fine. However, one must be cautious. Consider the following example:
Q = set of Rational numbers in the interval (0, 1), d( x, y) = | x – y| define a metric space ( Q, d).
What is bQ ? The closed interval [0, 1]. Further, iQ = {}. Thus we may think of the boundary of a set to be a 'thin set' object, which is clearly not so in this example. In fact, the bQ is a larger set than Q itself !
Fortunately, for objects in the Euclidean geometry (the 3D space denoting our familiar Euclidean geometry is denoted E3), the intuitive feel for these concepts is usually fine.
A metric space X is connected if it cannot be written as the union of two disjoint, non-empty open sets.
Consider two metric spaces, (X, d1) and (Y, d2). A function f: X à Y is a homeomorphism if f is continuous, and possesses an inverse which is also continuous. X and Y are then said to be homeomorphic.
It is often useful to think of homeomorphisms as 'elastic deformations' : the shape and the size etc may change, but the 'nearness' of points does not changes. Topology is the study of properties that remain invariant under homeomorphisms. For example, connectedness is a topological property.
We define an operation, regularization of a set X, denoted rX = kiX.
A set X is regular iff X = rX.
The class of regular sets is not closed under the normal set theory operations of difference (–), intersection (&) and complement (c). For example, let X = [0, 1] and Y = [1, 2]. Both X and Y are regular. But (X & Y) = {1}, and ( X – Y) = [0, 1); cX and cY are open; none of these four sets are regular.
For all the operations, k, c, i above, I consistently talk of a subset U of the underlying universal set, X of the metric space ( X, d). This is important because the metric is defined on elements of X. For example, if one talks of the subset [0,1] of the set of Reals, R, with the usual metric, then its interior is the open interval (0, 1). However, if we consider a line segment, say the closed line segment from the point (0, 0) to the point (1, 0) in the Euclidean 2D space, E2, with the Euclidean 2D distance metric, then the interior of this line is the null set !
In computational solid geometry (CSG), we plan to denote primitives as point sets. We shall construct solids out of set theoretic operations like union (U), difference (–), intersection (&) etc. It would be convenient if all the objects the CSG functions need to handle are regular. This is because the property of regularity makes it easier to compute object properties that we need to find about our solid models.
Hence we cannot use normal set theory operations in CSG – instead, we use ‘regularized set theoretic operations’, simply called Boolean operators, or regularized operators.
The regularized union (U*), regularized intersection (&*), regularized difference (-*) and regularized complement (c*) are defined as follows:
X U* Y = r( X U Y)
X &* Y = r( X & Y)
X -* Y = r( X – Y)
c* X = rcX
A very important property of the operators that a CAD system must provide is closure – that is, the output of applying the operator to an element (or elements) of the set is also an element of the set. This property is important for several reasons.
If we can develop a data structure to represent objects of a set, then the closure of the operators guarantees that all functions must only handle (and return) objects of the same type. We don’t need to program for ‘special case’ outputs.
It turns out that regularized operators can be used to model a large subset of all solid objects. What objects can (and what cannot) be represented by this model ? Roughly speaking, solid objects that can be described in a fairly compact way (e.g. listing an infinite number of points to make a point set is not too compact, but listing the equations of a few surfaces is fairly compact.) Also, objects that have a well behaved boundary. An example of a function that does not have a well-behaved boundary is sin(1/x), which, in the neighborhood of x = 0+, has an infinite number of very thin ‘slices’ of solid and air, and shown in the figure below.

Polyhedrons, and in general finite polynomial are well behaved functions, and fairly powerful in their ability to represent a large variety of shapes. Hence these are popular in most solid modeling systems.
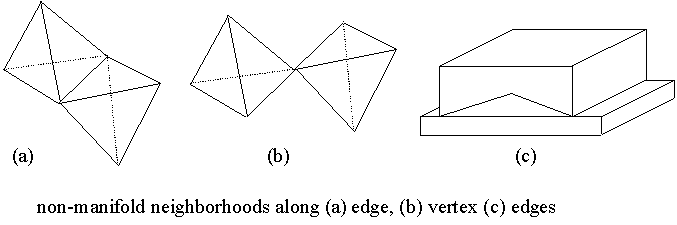
One limitation imposed by most solid modeling systems is that all objects handled by them must be topologically 'similar'. When dealing with solids, such objects are sometimes referred to as 2-manifolds. 'Topologically similar' requires some study, but intuitively, you can think of two objects being topologically similar if you can deform, stretch, or squeeze them and reach the same shape -- without having to (a) cut any portion, or (b) paste/glue any portions. For example, a coffee-mug and doughnut are topologically similar: you can deform and squeeze the 'mug' part of the coffee-mug and you will be left with the (doughnut shaped) handle. A ball and a cube are topologically similar. But a doughnut is not similar to a ball -- no matter how much you squeeze and bend, you cannot make a hole in the ball without making a cut or gluing.
Returning to manifolds (in particular, 2-manifolds), you think of a well behaved solid as a closed point set for which every point on the boundary has a neighborhood that is topologically similar to an open disk. There are some solid objects that do not meet this criterion -- these objects often cause trouble to CAD systems. Examples of some of these non-manifold (polyhedral) objects are shown in the figure below.
You will notice, in your work with practical solid modelers, that such applying operations that result in such conditions/shapes will often result in an error message (if you are lucky), or system hang-up.
References:
Introduction to Topology, G. F. Simmons
Fundamental concepts of geometry, Bruce E. Meserve
Several papers by H. B. Voelker and A. A. G. Requicha