
Design details of a part must include enough information to manufacture the part precisely. Projections provide a theoretically nice technique to draw precise 2D images of objects. However, the manufacturer needs more information. When machining a part, the manufacturer must know, for example, the distance between the centers of two holes. It is neither easy, nor accurate to measure the distance from the engineering drawing. Further, complex calculations may be required if the drawing uses non-orthographic projections. Therefore each drawing must carry enough dimensions to allow machining the part without needing to measure any dimension from the drawing.
The second problem relates to manufacturing - the probability to get the exact dimension specified (called the nominal dimension) is, of course, zero. So we must specify a range, and if the manufactured size is within this range, called the tolerance range, we will say that the produced part is 'acceptable'. The exact implications of this simple situation are very difficult to analyze. Firstly - how do we determine what is a good level of tolerance for a particular feature on the part? As we know, most modern manufacturing is based on two simple and powerful principles: division of labor and interchangeability. The correct specification of tolerance is related to the issue of interchangeability.
From a design point of view, tight tolerance ranges are often better (less vibration, less wear, less noise). From a manufacturing point of view, large tolerances are better (easier to machine, faster to produce, easier to assemble). Therefore, specification of the tolerance requires some knowledge of what level of accuracy and repeatability can be provided by the manufacturing processes that are available. This is an important reason why most companies adopt Concurrent engineering - during the design specification, the manufacturing engineer can tell the designers how much it will cost if they specify a particular tolerance, or whether some design can be made with the available machines.
Our motivation here is to study some basics principles of design representations. This is in three parts:
We want to make 2D images of 3D objects. Our images must convey feasible 3D objects, not the kind in the figures below!


Durer's machine was a mechanical technique to draw what we call perspective projections. These were very important in 14th century Europe, when several very large buildings were being constructed in various rich cities (especially in Italian cities like Florence and Rome, where many large gothic churches were being commissioned by the royalty). The architects first made perspective views showing their design ideas, before they could be approved. This is also the time when the theory of perspectives was developed in geometry. Modern CAD systems use this theory for perspective transformations that are used not only in 3D rendering and image processing, but also in the mathematics of complex curved surfaces that are represented by rational polynomial functions called NURBS (Non-Uniform Rational B-Splines).
The idea of perspective maps is based on human sight and perception. Humans perceive the size of an object by the size of its image on our retina. So different sized objects may project the same size image on our eyes (which is why we cannot judge size of objects if we can't perceive how far they are.)

Likewise, the same size object looks smaller as it goes further, as seen in the following picture.

As the object goes farther, it makes smaller and smaller image on the retina, until, at some stage, we cannot distinguish it from a point. In other words, a parallel line will seem to converge to a point at this distance. This point is called a vanishing point (or station point), and different choices of the vanishing point give different effects on perspective projections.

The picture above is interesting. Notice that the image on the plane called the 'picture plane' is a perspective map of the 3D object behind it. Of course, the object itself is also in the picture, and is therefore a 2D map!
Is the object in perspective view ?
It is not. This can be seen from the fact that parallel lines on the
object remain parallel. Let us explore this image
a little more, and see what we can do with it..

In the second figure, we see a perspective with two vanishing points. Similarly, we could make perspectives with three vanishing points. While perspective views are excellent for rendering, and for architecture, they are not so popular for mechanical drafting. Mechanical drawings are not used so much for realistic images, but more to convey exact dimensions in a clear, and easy to draw method. In fact, since parallel lines do not remain parallel after perspective mapping, they may even be misinterpreted by the machinist. Therefore, in the above figure, the first format is more convenient for mechanical drawings - easier to draw, and less likely to be misinterpreted. A common convention for mechanical drawings, therefore, is to find mapping where parallel lines remain parallel after the mapping. This is achieved simply by allowing the vanishing point to locate at infinity. Such a map will produce an orthographic view.
Another problem with a mapping is that we can only see whatever side of the object is close to the projection plane. But what about the back side (in general, all surfaces that cannot be seen from a given viewing position are called hidden surfaces.) There may be features on hidden surfaces whose details must be provided to the machinist. Hence, we draw more than one view. Typically, three views are sufficient from many parts, although sometimes we need several more views (e.g. auxiliary views and section views) to complete the specifications. The following figure illustrates the idea of orthographic views.

Orthographic views are the language of engineering communication. Since more complicated objects are difficult to visualize from orthographic views, typically an isometric view is provided. Notice that orthographic views of an object will be different if the object is rotated with respect to the picture plane. The convention used to fix the orientation is to locate the picture box such that its planes are parallel to as many faces on the part as possible. For rotational parts, it is conventional to choose the axis of rotation to be in true length in two views, and a point in the third (see figure below).

Instead of using the above convention for finding the orientation of the part, we could rotate the part in such a way as to give a better 3D effect. One way to fix this orientation is the isometric view -- an orthographic view of the part oriented so that a cube in the obvious orientation will show each edge shortened by exactly the same amount.

If we generalize the idea of the isometric, we get axonometric projections: if the foreshortening of unit length along the three axes are all different, we get tri-metric projections; if the foreshortening along two axes is same, and along the third is different, we get di-metric projections). Another popular view is oblique projection - in this case, the front view is in true size, and all lines perpendicular to the front plane are projected at the oblique angle. The figure below shows these ideas.

In all cases of projections to represent objects, engineering drawings must be made to scale - that is, the length of each line on the drawing must be a function of the projective technique used and the actual size of the line on the 3D part. The formula used must be the same for each line on the part.
A machinist must be told the exact size of all important features on apart - this is done by specification of dimensions. To avoid confusion, all dimensions are specified by following rules. We look at a popular standard for specification of dimensions - the ANSI 14.5m standard.
Datum: A theoretical geometric object (point, line, axis, or plane) derived from a specific part/feature of a datum feature on the part. A datum is used for two purposes - either to specify distance of a feature from the datum, or to specify some geometric characteristic (e.g. roughness) of a feature.
Datum feature: An actual feature of a part, that is used to establish a datum.
Basic Dimension: A numerical value specifying the theoretically exact size, profile, orientation, or location of a feature or datum target. Allowable variations on this size are specified by means of tolerances on the basic dimension.
Feature: Some meaningful portion of the part, such as a hole, an axis of a hole, a plane, an edge etc.
Limits: The maximum and minimum size (or extreme positions of planes etc) allowable for a feature whose dimension and tolerance have been specified. The largest (maximum allowable size) is the upper limit and the least allowable size is the lower limit.
LMC (Least Material Condition): The condition is which the feature size contains the least amount of material. For a hole, this happens when it is at the upper limit; for a shaft, or cylinder, this happens when it is at the lower limit.
MMC (Maximum material Condition): The condition is which the feature size contains the maximum amount of material. For a hole, this happens when it is at the lower limit; for a shaft, or cylinder, this happens when it is at the upper limit.
Conventions for dimensioning: There are several rules; the ones I think are most important are listed below:
In some cases, redundant dimensions are written on the drawing - these are called reference dimensions, written inside parentheses, and are specified without tolerance values.
The figure below shows a simple example demonstrating good dimensioning practices. Notice how most dimensions are measured off the left edge in the top view, and the top edge in the top view - the corresponding surfaces therefore may be used as datum surfaces. In most cases, such datum surfaces must be marked, since the machinist will first machine these surfaces smoothly, and then use them to measure distances of all other features.


Conventional Tolerancing:
Historically, the study of tolerance specification became important along
with the importance of mass production - since tolerance driven manufacturing
enables interchangeability. In the early days, the most important tolerance
control was seen in:
(a) Size of a feature
The size of a feature was specified by a nominal size, and the allowed variation, as follows: 2.50±0.03, which means that if the actual size of the object, after it is manufacture, is any value between 2.47 and 2.53, the part is acceptable. In this expression, 2.50 is the basic size; ±0.03 is the tolerance; 2.53 is the upper limit, 2.47 is the lower limit; The number of digits following the decimal point indicate the level of precision. Sometimes, we write this dimension as 2.5, which is the nominal size of the feature.
Tolerances can be specified as bilateral variations, or unilateral variations (each example below represents the same specification).

(b) The type of fit between mating features
This is restricted mostly to hole-in-shaft type of fits, since these are most common in design. The nominal size is based on the functional requirements; then the designer needs to specify the basic diameter and tolerance of the shaft, S±s/2, and the hole, H±h/2. These values must be determined by functional as well as manufacturability. The classes of fits and their characteristics are shown below. Notice that interference fits have negative allowance value, using the definition: a = min hole dia - max shaft dia.

When specifying tolerances, it is common to specify the basic size of the hole, and then derive the other dimensions to be specified based on the fit required. This is because holes are manufactured using standard sized tools, while the diameter of a shaft can be controlled with great accuracy during the turning operation. Some possible methods of specification of tolerances for different fits are shown below.

The idea of hole-basic or shaft-basic is generalized as follows: the Maximum (or Least) material condition refers to the size of the feature when the part has the maximum (or Least) amount of material. Thus a hole is at maximum material condition (MMC) when it is at the lower limit of it size; the hole is at least material condition (LMC) when it is at the upper limit. Similarly, a shaft is a MMC at its upper limit, and at LMC at its lower limit.
Geometric Tolerancing
Conventional tolerancing had several problems that were addressed later by geometric tolerancing. These problems included:

Geometric tolerancing uses conventional tolerancing ideas, and adds many other important specifications.
Datums: A datum is a theoretical feature (e.g. plane, line) that serves as a global coordinate frame for the part during different activities such as design, manufacturing and inspection. Thus, the different features on a part (surfaces, planes, axes) are designed with respect to the datums (e.g. by specifying the distance of a plane from a datum plane). During manufacturing, the actual features corresponding to the datum are established using specially machined blocks (gauge blocks, set blocks, sine-blocks etc.), or by using position sensors. The actual size of all other measurements is measured with respect to such references. Similar blocks and gauges are used during inspection. Therefore each design must specify the datum planes (or features). The actual plane on the part (which always some roughness, however small) corresponding to a (theoretical, and therefore perfect) datum plane is called a datum feature. Therefore, the specification of datum features must also describe their relative importance. For instance, we may define three mutually perpendicular planes on the part as datum features A, B and C, and then define A as the primary datum feature, B as secondary, and C as tertiary. This sequence is important in eliminating errors of measurement between different applications (see figure).

When measuring, it is important to first establish datum feature A (three points on the surface will contact the reference plane), next establish datum feature B (two points on feature B will contact with reference plane B), and finally establish datum feature C (one point of contact). This is the basis of the common 3-2-1 principle in fixturing.
The following figure summarizes ANSI symbols for geometric tolerancing.
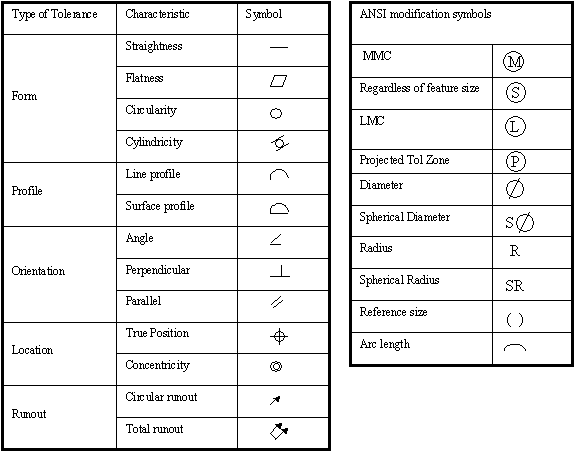

Location tolerances: location tolerances in the conventional system cause rectangular tolerance zones for the point being located. It s more common nowadays to use a different type of location tolerance specification, called True Position, which specifies that the distance between the position and the target in any direction must not exceed the specified tolerance. This obviously leads to a circular (or cylindrical) tolerance zone. The following figure shows an example.

[source: Ibrahim Zeid, CAD/CAM: Theory and Practice, McGraw Hill]
Form Tolerances: modern manufacturing requires precise control over the form and shape of many surfaces, and also on the geometry and location of features with respect to other features. Such control can be specified by the use of form tolerances. The following figures show the meaning and specification of different form tolerances.



[source: Ibrahim Zeid, CAD/CAM: Theory and Practice, McGraw Hill]
ANSI 14.5M Dimensioning and Tolerancing, ASME press
NURBS Curves and Surface, Gerald Farin, A. K. Peters Ltd
CAD/CAM Theory and Practice, Ibrahim Zeid, McGraw hill
Engineering Drawing and Graphic Technology, T. E. French and C. J. Vierck, McGraw Hill
Engineering Graphics, F. E. Giesecke et al, Prentice Hall
Daryl Holstrom (the Rails picture, amusingly titled 'light at the end of the tunnel')